Comprehensive Professional Guide
to the ABHP Part II Examination

Parent-Daughter Equilibria

The activity of a daughter nuclide, $A_2$, at time t is given by the Bateman equation:

• Transient Equilibrium ($T_{1} > T_{2}$): Occurs when the parent is longer-lived than the daughter (e.g., ${}^{99}$Mo/${}^{99m}$Tc). After several daughter half-lives, the daughter appears to decay with the parent's half-life. The activity ratio becomes constant: $\frac{A_2}{A_1} = \frac{\lambda_2}{\lambda_2 - \lambda_1}$.
• Secular Equilibrium ($T_{1} \gg T_{2}$): Occurs when the parent is much longer-lived (e.g., ${}^{90}$Sr/${}^{90}$Y). At equilibrium, the activities become equal: $A_2 \approx A_1$.

Decay Schemes & Nuclear Transitions

Beyond simple decay, you must understand the processes by which an excited nucleus reaches its ground state.

• Gamma Emission: An excited nucleus releases energy by emitting a photon (gamma ray) of a discrete energy corresponding to the difference between nuclear energy levels.
• Internal Conversion (IC): An excited nucleus transfers its energy directly to an orbital electron (usually from the K or L shell), ejecting it from the atom. This is a radiationless transition and is competitive with gamma emission. The ejected electron is called a conversion electron. IC is more probable in high-Z nuclei and for low-energy transitions.
• Isomeric Transition (IT): Occurs in nuclides with a metastable state (e.g., ${}^{99m}$Tc, ${}^{137m}$Ba). The nucleus remains in an excited state for a measurable half-life before de-exciting, typically via gamma emission or internal conversion.

Neutron Sources & Interactions

• Sources: Be familiar with common neutron sources:
  • Spontaneous Fission (SF): e.g., ${}^{252}$Cf.
  • $(\alpha, n)$ Reactions: An alpha emitter mixed with a light element, e.g., AmBe or PuBe.
  • Photoneutron $(\gamma, n)$ Reactions: High-energy photons (>~8 MeV) interacting with matter, common around high-energy accelerators.
• Interactions:
  • Elastic Scattering: "Billiard ball" collision where kinetic energy is conserved. This is the primary mechanism for moderating (slowing down) fast neutrons, and it is most efficient with low-Z materials (like hydrogen in water or polyethylene).
  • Inelastic Scattering: The neutron is captured and re-emitted with lower energy, leaving the target nucleus in an excited state. This has an energy threshold and is important for fast neutrons in high-Z materials.
  • Radiative Capture $(n, \gamma)$: The dominant interaction for thermal neutrons. The nucleus absorbs the neutron and emits a prompt gamma ray. This is the basis for most activation calculations.

Photon Interactions: The "Big Three"

Understanding the relative importance of the three main photon interactions is crucial for shielding, dosimetry, and detector selection.

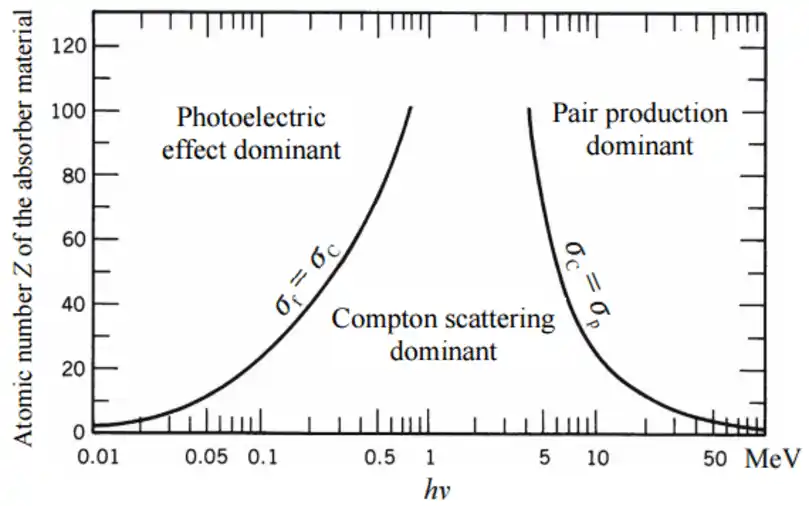
• Photoelectric Effect: An "all or nothing" absorption of a photon by a bound atomic electron. It is the dominant interaction for low-energy photons and in high-Z materials. The cross-section is approximately proportional to $\frac{Z^4}{E^3}$. This interaction is responsible for the high efficiency of NaI detectors at low energies and the effectiveness of lead shielding.
• Compton Scattering: An interaction with a "free" or loosely-bound electron. The photon scatters at an angle, losing some of its energy to the recoil electron. It is the dominant interaction for mid-energy photons (approx. 0.5-5 MeV) in most materials, including tissue. This is the primary source of scatter in shielding and the physical basis for the Compton continuum in a gamma spectrum.
• Pair Production: A high-energy photon interacts in the electric field of a nucleus and is converted into an electron-positron pair. It has a strict energy threshold of 1.022 MeV. The positron subsequently annihilates, producing two 0.511 MeV photons. This interaction is dominant for high-energy photons in high-Z materials.

Photon Interaction Dominance

Being able to sketch the regions of dominance for the "Big Three" interactions as a function of photon energy and absorber atomic number (Z) is a classic exam topic.

Attenuation vs. Absorption Coefficients

It is critical to distinguish between the linear attenuation coefficient ($\mu$) and the energy absorption coefficient ($\mu_{en}$).

• Linear Attenuation Coefficient ($\mu$): Describes the fraction of photons removed from a narrow beam per unit thickness. It includes all interactions (photoelectric, Compton, pair production). It is used for shielding calculations: $I = I_0 e^{-\mu x}$.
• Energy Absorption Coefficient ($\mu_{en}$): Describes the fraction of photon energy that is deposited in the material via the kinetic energy of secondary electrons. It is always less than $\mu$ because it excludes the energy carried away by scattered photons, annihilation photons, and bremsstrahlung. It is used for calculating KERMA and absorbed dose.

Charged Particle Interactions

• Linear Energy Transfer (LET): The average energy deposited by a charged particle per unit path length. High-LET radiation (alphas, protons) is more biologically damaging than low-LET radiation (betas, gammas) for the same absorbed dose.
• Bragg Peak: Heavy charged particles (alphas, protons) deposit the majority of their energy at the very end of their track. This peak in energy deposition is called the Bragg peak and is the principle behind proton therapy.
• Beta Spectrum: Beta particles are emitted with a continuous spectrum of energies up to a maximum ($E_{max}$). This is because the decay energy is shared with a neutrino. This continuous spectrum is why beta attenuation in matter appears roughly exponential, even though individual electrons have a finite range.

Bremsstrahlung Production

Bremsstrahlung ("braking radiation") is produced when a high-energy charged particle (typically an electron) decelerates rapidly in the electric field of a nucleus. This is a key consideration for beta shielding.

• Energy Dependence: The fraction of energy lost to bremsstrahlung is proportional to the initial electron energy (E) and the atomic number (Z) of the absorber: $$f \approx \frac{ZE}{800}$$
• Shielding Implication: To shield high-energy beta emitters (e.g., Sr-90/Y-90), a low-Z material (like plastic or aluminum) should be used as the primary shield to minimize bremsstrahlung production. A high-Z material (like lead) can then be placed outside the low-Z shield to attenuate the bremsstrahlung x-rays produced.

The Buildup Factor (B)

The simple exponential attenuation equation, $I = I_0 e^{-\mu x}$, is only valid for narrow-beam conditions. For shielding calculations, you must account for scattered photons.

• Physical Basis: The buildup factor is a dimensionless multiplier ($B \ge 1$) that corrects the narrow-beam equation for the additional dose contribution from photons that have undergone Compton scattering within the shield but still reach the point of interest.
• Dependencies: B is a function of the initial photon energy, the shield material (Z), and the shield thickness in mean free paths ($mfp = \mu x$).
• Layered Shields: For a multi-layered shield, a common approximation is to use the buildup factor for the *final* material, but calculate it using the total number of mean free paths for the *entire* shield composite.

The ICRP 30 vs. ICRP 66+ Respiratory Tract Models

The exam questions are based on the ICRP 26/30 system, but awareness of the newer models shows advanced knowledge.

• ICRP 30 Model: A simple three-compartment model (Nasopharyngeal, Tracheobronchial, Pulmonary). Material is cleared from each region by mechanical processes or absorption into blood, with fixed rates for solubility classes D, W, and Y.
• ICRP 66+ Model: A much more detailed anatomical model (ET1, ET2, BB, bb, AI regions). It treats clearance as a competition between mechanical transport (e.g., mucus escalator) and absorption into blood. It replaces solubility classes with absorption Types F (Fast), M (Medium), and S (Slow). This model provides more realistic, particle-size-dependent dose estimates.

Medical Interventions

For significant intakes, certain medical countermeasures can reduce the resulting dose.

• Blocking Agents (e.g., KI): Saturates the target organ (thyroid) with stable iodine, preventing the uptake of radioactive iodine. Must be administered *before or very shortly after* the intake to be effective.
• Chelation Therapy (e.g., DTPA): Binds with transuranics (Pu, Am) in the bloodstream to form a stable complex that is rapidly excreted. It is most effective when given quickly after an intake of *soluble* material.
• Lung Lavage: A high-risk medical procedure to physically wash *insoluble* material out of the lungs. Only considered in cases of extremely high, life-threatening intakes.

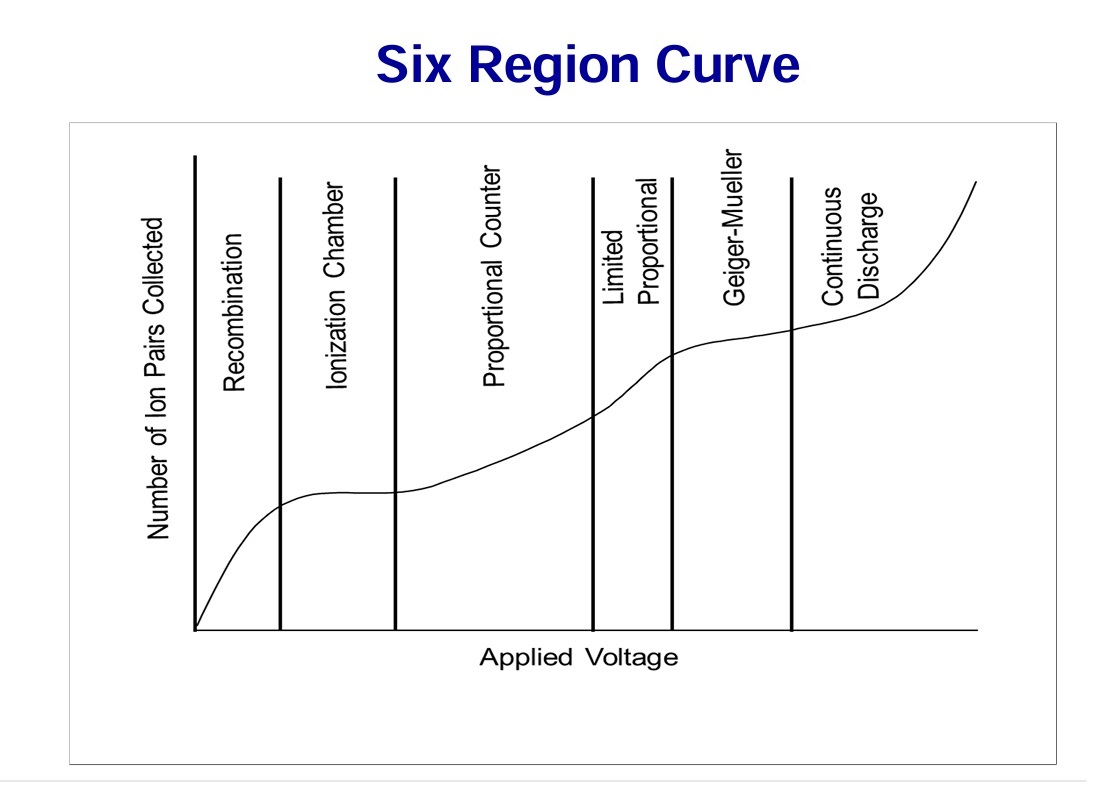
The Six-Region Curve

You must be able to identify and explain each region of the characteristic curve of pulse amplitude vs. applied voltage: Recombination, Ionization, Proportional, Limited Proportional, Geiger-Mueller (GM), and Continuous Discharge.

Proportional Counters

Operating in the proportional region allows for energy discrimination. The pulse height is proportional to the initial energy deposited.

• Gas Multiplication: Unlike ion chambers, the applied voltage is high enough to accelerate primary electrons, causing them to create secondary ionizations. This "gas amplification" (typically $10^2$ to $10^4$) results in a much larger, but still proportional, output pulse.
• Applications: Because they can distinguish between particle energies, proportional counters are excellent for spectroscopy of low-energy radiations (alphas, betas) and for discriminating between them (e.g., alpha counting in the presence of a high beta background).

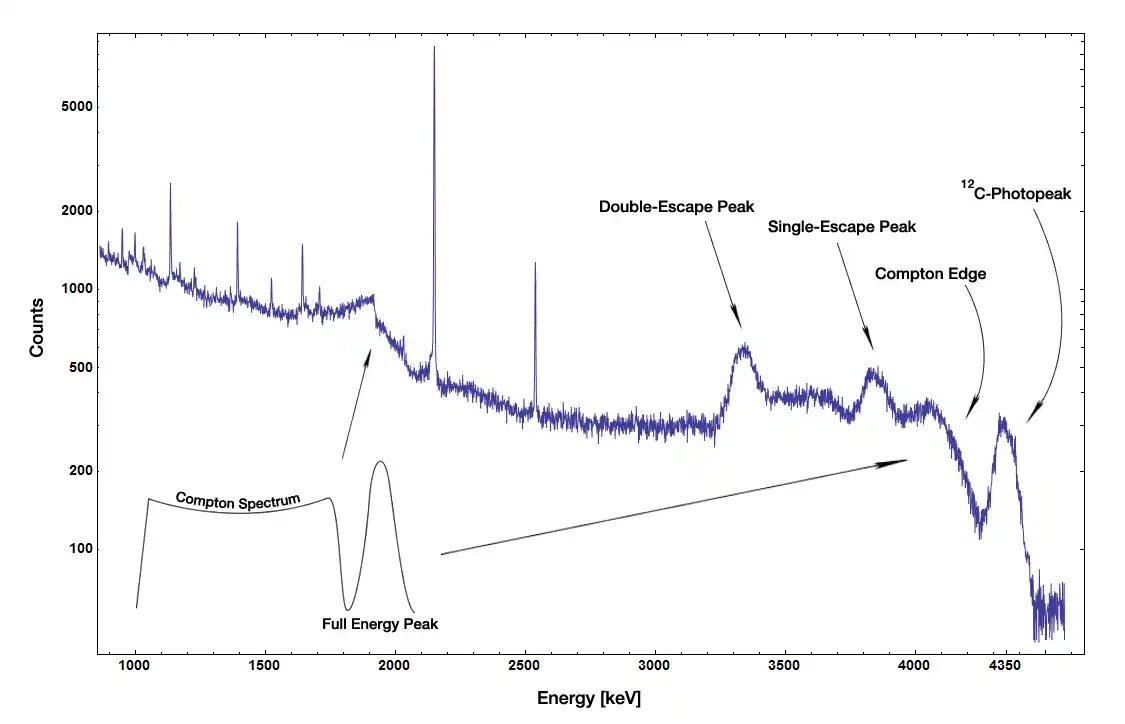
Gamma Spectroscopy

You must be able to identify all key features on a gamma spectrum. The diagram below shows a representative spectrum from a high-resolution detector.

Semiconductor Detectors (HPGe)

High-Purity Germanium (HPGe) detectors are the gold standard for gamma spectroscopy.

• Superior Resolution: The energy required to create an electron-hole pair in germanium (~3 eV) is much lower than the energy to create an ion pair in a gas or a photoelectron in a scintillator. This results in a much larger number of charge carriers for a given photon energy, leading to vastly superior energy resolution (sharper peaks).
• Trade-offs: HPGe detectors are more expensive than NaI scintillators, have lower efficiency (due to smaller crystal sizes), and must be cooled to liquid nitrogen temperatures to reduce thermal noise.

Liquid Scintillation Counting (LSC)

This is the method of choice for low-energy beta emitters (${}^3$H, ${}^{14}$C). The most critical concept is **quenching**, any process that reduces light output. To get an accurate DPM, you must determine the efficiency for each *quenched* sample, typically by using an instrument-generated quench curve.

Neutron Detector Principles

• Slow/Thermal: Use high cross-section reactions like ${}^{10}B(n,\alpha)$ or ${}^{3}He(n,p)$. Be prepared to explain the "wall effect," where a reaction near the detector wall results in incomplete energy deposition and a smaller pulse.
• Fast: Use moderation (e.g., Bonner spheres) to thermalize neutrons before detection, or use proton recoil detectors.
• Bonner Spheres: A set of polyethylene spheres of different diameters with a thermal neutron detector (like a LiI scintillator) at the center. The varying moderator thickness makes each sphere most sensitive to a different neutron energy. By taking measurements with multiple spheres and using an "unfolding" algorithm, one can reconstruct the neutron energy spectrum.

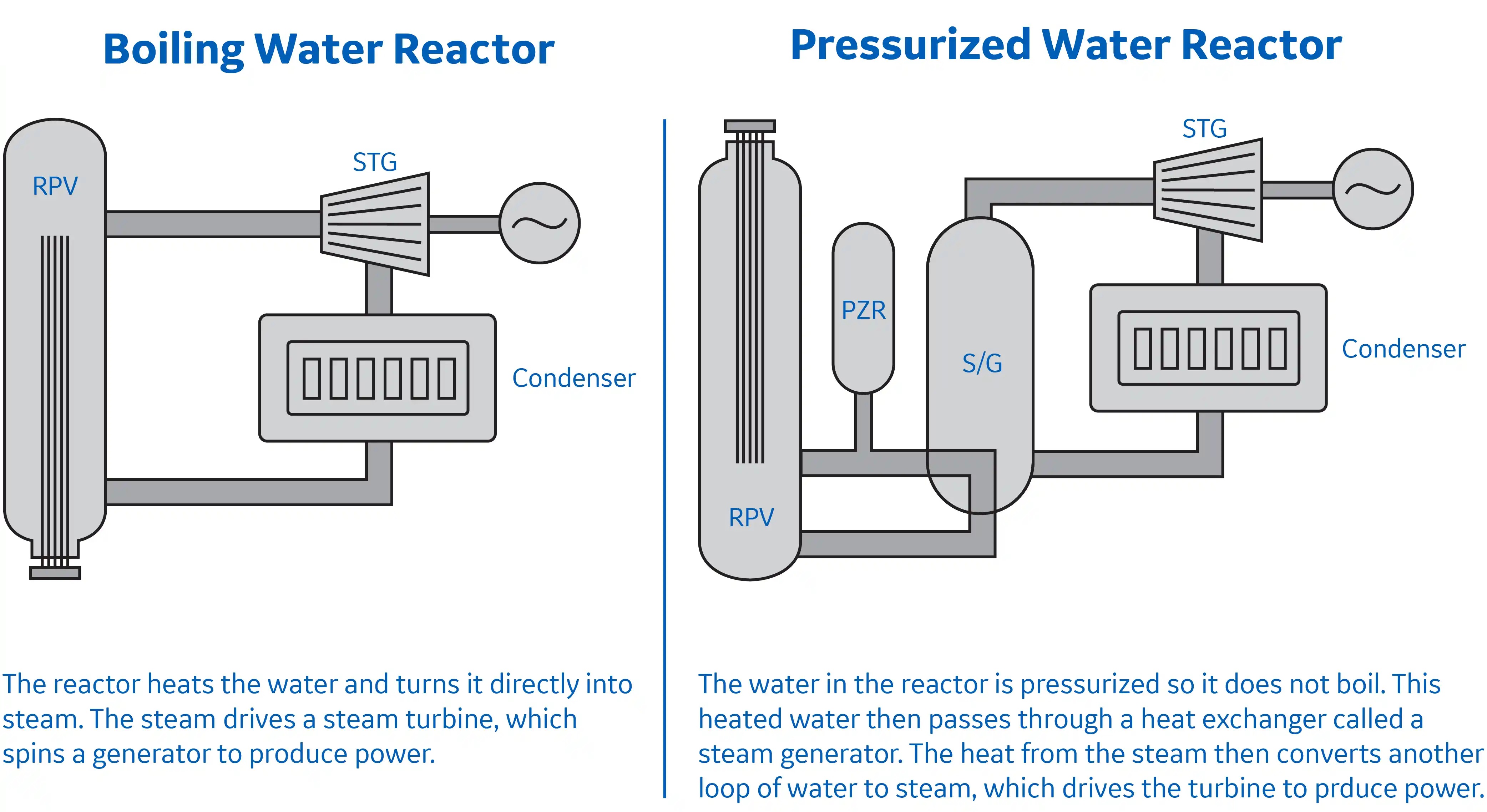
PWR vs. BWR Radiological Characteristics

Understanding the fundamental design differences is key to understanding their radiological signatures.

• Pressurized Water Reactor (PWR): The primary coolant loop is separate from the secondary loop that drives the turbine. The primary coolant is kept under very high pressure to prevent boiling. This design contains most of the fission and activation products within the containment building.
• Boiling Water Reactor (BWR): The water boils directly in the reactor vessel, and the resulting steam is sent directly to the turbine. This means that any radionuclides in the coolant are transported throughout the steam cycle, leading to contamination and radiation fields in the turbine building. The most significant radiological issue during operation is the creation of ${}^{16}\text{N}$ (from the ${}^{16}O(n,p){}^{16}N$ reaction), a high-energy (6.1 MeV) gamma emitter with a very short (7.1 s) half-life, which causes "turbine shine."

CRUD and Source Term Management

CRUD (Chalk River Unidentified Deposits) refers to activated corrosion products that are the primary source of occupational dose during reactor outages.

• Formation: Metal components (pipes, valves) corrode, releasing ions (e.g., Co, Ni, Fe) into the primary coolant. These ions circulate through the reactor core, where they are activated by the intense neutron flux.
• Deposition: These now-radioactive ions deposit on surfaces throughout the primary system, creating high dose rate "hot spots." ${}^{60}$Co is the most significant long-term contributor to this dose.
• Control: Source term reduction strategies, such as controlling coolant chemistry (e.g., pH) and using materials with low cobalt content, are critical ALARA measures.

MARSSIM Process Overview

The Multi-Agency Radiation Survey and Site Investigation Manual (MARSSIM) provides a standard, technically defensible methodology for demonstrating compliance with a dose- or risk-based regulation. It is essential for decommissioning and license termination (e.g., per 10 CFR 20 Subpart E).

• Data Quality Objectives (DQOs): A 7-step planning process to ensure that the type, quantity, and quality of data collected are appropriate for the decision to be made. The steps include: stating the problem, identifying the decision, identifying inputs, defining boundaries, developing a decision rule, specifying error tolerances, and optimizing the design.
• Area Classification: Areas are classified based on their potential for contamination, which directs the level of survey effort (i.e., the number of samples).
  • Class 1: Highest potential for contamination (e.g., > DCGL); requires the highest survey density.
  • Class 2: Lower potential for contamination, but still some potential for levels > DCGL.
  • Class 3: Lowest potential; not expected to contain any residual radioactivity above background.
• Survey Design: The FSS typically uses a systematic grid sampling pattern to ensure full coverage and avoid bias.

The Gray Region & Decision Errors

A key concept in MARSSIM survey design is the "Gray Region," which is the range of concentrations between the Lower Bound of the Gray Region (LBGR) and the DCGL. This is the range where decision errors are most likely to occur. The width of this region ($\Delta = DCGL - LBGR$) is a critical input for calculating the required number of samples. A smaller gray region (a more stringent survey) requires more samples to achieve the desired statistical confidence.

MARSSIM Statistical Tests

Because measurements have uncertainty, statistical tests are required to make a decision with a known level of confidence. The **null hypothesis ($H_0$)** is always that the survey unit **exceeds** the release criterion.

• Sign Test: A simple non-parametric test used when the contaminant is not present in background. It compares each measurement directly to the DCGL. The goal is to reject $H_0$.
• Wilcoxon Rank Sum (WRS) Test: A non-parametric test used when the contaminant *is* present in background. It compares the distribution of measurements from the survey area to the distribution of measurements from a clean reference (background) area to determine if the survey area is statistically "dirtier" than the reference area.
• Decision Errors: You must know the definitions of Type I ($\alpha$) and Type II ($\beta$) errors.
  • Type I Error ($\alpha$): Deciding the survey unit is clean when it is actually dirty (a "false positive" for the cleanup). This is the error MARSSIM primarily seeks to control.
  • Type II Error ($\beta$): Deciding the survey unit is dirty when it is actually clean (a "false negative" for the cleanup, leading to unnecessary remediation).

RESRAD

The **RESRAD (RESidual RADioactivity)** family of computer codes, developed by Argonne National Laboratory, are the standard tools used to perform the pathway analysis needed to derive site-specific DCGLs. The codes model the transport of radionuclides from soil and surfaces through multiple environmental pathways (e.g., groundwater, plant uptake, inhalation, direct exposure) to calculate a dose to a defined human receptor.

Key Principles

The goal of an environmental monitoring program is to verify effluent controls, detect unexpected releases, and assess public dose.

• Indicator Locations: Placed where concentrations are expected to be highest based on modeling (e.g., downwind, downstream).
• Background Locations: Placed far from the site, in a location that is unimpacted by site activities, to measure natural background levels for comparison.
• Sample Media: Air, water (surface and ground), soil, sediment, and biota (e.g., vegetation, fish) are chosen based on the expected radionuclides and the most likely exposure pathways to the public.

The Six-Factor Formula and $k_{eff}$

The state of a fissile system is defined by the effective multiplication factor, $k_{eff}$, which is the ratio of neutrons in one generation to the generation before. $k_{eff} = k_{\infty} \cdot P_{NL}$, where $P_{NL}$ is the non-leakage probability.

• $k_{eff} < 1$: Subcritical. The chain reaction will die out.
• $k_{eff} = 1$: Critical. The chain reaction is self-sustaining.
• $k_{eff} > 1$: Supercritical. The chain reaction will rapidly increase in power.

The "Six Factors" are the physical parameters that are controlled to keep $k_{eff}$ safely below 1:

1. Mass: Controlling the total amount of fissile material to stay below the critical mass for a given configuration.
2. Geometry: Using "geometrically favorable" shapes (e.g., thin slabs, long narrow cylinders) that maximize neutron leakage. A sphere is the most reactive geometry.
3. Moderation: Controlling the presence of hydrogenous materials (water, oil, plastic) that slow neutrons down to thermal energies, where the fission cross-section is much higher.
4. Reflection: Controlling the proximity of materials (water, concrete, steel) that can scatter neutrons back into the fissile material, effectively reducing the critical mass.
5. Concentration/Density: Ensuring the density of fissile atoms is below the critical value. This can involve mixing with non-fissile materials.
6. Interaction/Poisons: Using materials with very high neutron absorption cross-sections (e.g., Boron, Cadmium, Gadolinium) to act as "poisons," removing neutrons from the system. Also includes ensuring safe spacing between multiple subcritical units.

The Double Contingency Principle

This is the fundamental safety philosophy in criticality safety. It requires that a process be designed to be safe, assuming that **two independent, concurrent, and unlikely changes** in conditions have occurred before a criticality accident is possible. In practice, this means that no single error or equipment failure should be able to cause a criticality.

Laser Safety (ANSI Z136.1)

Laser safety focuses on preventing thermal or photochemical damage to the eye and skin.

• Maximum Permissible Exposure (MPE): The fundamental limit. It is the level of laser radiation to which a person may be exposed without hazardous effect or adverse biological changes in the eye or skin. It depends on wavelength, exposure duration, and whether the source is point or extended. An MPE table will always be provided.
• Nominal Ocular Hazard Distance (NOHD): The distance along the axis of the laser beam beyond which the beam irradiance or radiant exposure is less than the MPE.
• Laser Classifications: Know the general hazards of each class. Class 1 is safe for viewing. Class 2 is safe for momentary viewing due to the aversion response (0.25 s). Class 3R (formerly IIIa) is marginally unsafe for direct viewing. Class 3B (formerly IIIb) is hazardous for direct viewing. Class 4 is a hazard from direct, specular, and diffuse reflections and can be a fire hazard.

RF/Microwave Safety

The primary hazard from RF/microwave radiation is heating of body tissues.

• Near-Field vs. Far-Field: The boundary between the two is roughly at $R = \frac{2D^2}{\lambda}$, where D is the antenna diameter and $\lambda$ is the wavelength. In the far-field, the beam behaves as a plane wave and power density (S) decreases with the inverse square of distance ($1/d^2$). In the near-field, the relationship is complex, and direct measurements of both E- and H-fields are necessary.
• Specific Absorption Rate (SAR): The primary dosimetric quantity for RF exposure. It is the rate at which energy is absorbed per unit mass of body tissue, measured in watts per kilogram (W/kg). Exposure limits are based on keeping the whole-body average SAR below a certain level (e.g., 0.4 W/kg for controlled environments).

Ultraviolet (UV) Radiation Safety

UV radiation is typically categorized by wavelength, with each category having different penetration abilities and biological effects.

• UVA (315-400 nm): Long-wave UV, often called "black light." It penetrates deepest and is primarily associated with skin aging and wrinkling.
• UVB (280-315 nm): Mid-range UV, which is the primary cause of skin reddening (erythema) and sunburn. It is also the main cause of most skin cancers.
• UVC (100-280 nm): Short-wave UV, which is the most damaging but is almost completely absorbed by the Earth's ozone layer. It is commonly found in germicidal lamps. The primary hazards are to the eye (photokeratitis) and skin (erythema).

Key Update: ICRP 60 vs. ICRP 103

While U.S. regulations (10 CFR 20) are based on ICRP 26/30 and 60, a modern CHP should be aware of the 2007 recommendations in ICRP 103.

• Tissue Weighting Factors ($w_T$): ICRP 103 updated the list of tissues and their weighting factors. For example, the gonad weighting factor was reduced from 0.20 to 0.08, while breast was increased from 0.05 to 0.12. A "remainder" category was also changed.
• Radiation Weighting Factors ($w_R$): The concept of a continuous Quality Factor Q(L) was replaced with specific $w_R$ values for radiation types (e.g., 20 for alpha particles, a continuous function for neutrons).
• Effective Dose: The term "Effective Dose" (E) is used instead of "Total Effective Dose Equivalent" (TEDE), though the concepts are functionally similar for regulatory purposes.

Planned Special and Emergency Exposures

Situations may arise where exceeding the standard occupational dose limits is necessary. These are tightly controlled.

• Planned Special Exposure (PSE): Authorized by a licensee in advance for an exceptional situation. Per 10 CFR 20, a PSE is allowed only if it does not exceed the annual limits (5 rem TEDE, 50 rem to any organ) and the lifetime dose from all PSEs does not exceed 5 times the annual limit (i.e., 25 rem TEDE).
• Emergency Worker Guidelines (NCRP/EPA): These are not regulations but guidance for emergency response.
  • ~10 rem: All activities during an emergency.
  • ~25 rem: Protecting valuable property.
  • >25 rem (up to ~100 rem): Lifesaving activities or protecting large populations, only for volunteers who are fully aware of the risks.

The Sum of Fractions Rule

To control exposure to multiple sources (internal or external), the sum of the ratios of the exposure to the applicable limit must not exceed 1.

Dose Limits for Members of the Public

• The annual limit is 0.1 rem (1 mSv) TEDE from licensed operations.
• The dose rate in any unrestricted area from an external source must not exceed 2 mrem in any one hour.
• Effluent Concentration (EC) values in 10 CFR 20 Appendix B are derived such that if a member of the public were continuously exposed to that concentration in air or water, they would not exceed the 0.1 rem annual limit.
• The limit for license termination (decommissioning) is **25 mrem/year** to an average member of the critical group (10 CFR 20.1402).

Order of Magnitude Estimations

Before beginning a complex calculation, perform a quick, "back-of-the-envelope" estimate to determine if your potential answer is reasonable. This can prevent significant errors caused by unit conversions or calculator mistakes. Use rules of thumb and round constants to simplify the math (e.g., $\pi \approx 3$).

Example: If asked for the dose rate from 1 Ci of Co-60 at 1 meter, you should immediately know the answer is ~1.3 R/hr. If your detailed calculation yields a result in the mR/hr or thousands of R/hr, you have made an error.

Working Backwards from the Answer

For multi-step problems, a useful strategy is to start with the final desired quantity and work backwards to the information you are given.

1. Identify the Goal: What is the final unit and quantity you need to calculate (e.g., CEDE in rem)?
2. Find the Final Equation: What is the immediate precursor formula to get that answer? (e.g., $CEDE = (\text{Intake}/ALI) \times 5$ rem).
3. Assess Inputs: For each input in that formula (Intake, ALI), is it given or does it need to be calculated?
4. Repeat: For each input that must be calculated, repeat the process, identifying the precursor formula and its inputs, until you have a chain of calculations that connects the initial given information to the final answer.

Building Equations from Scratch

On the exam, you may not be given the exact formula you need. A critical skill is the ability to derive a formula on the fly using dimensional analysis (i.e., making sure the units cancel correctly). Start with what you're given, what you need to find, and then find the conversion factors and constants that bridge the gap.

Example: Derive an equation for the dose rate (mrem/hr) at 1 meter above an infinitely large, uniformly contaminated surface, given the contamination level in dpm/100 cm².

1. Start with the Goal Unit: $\frac{mrem}{hr}$
2. Introduce the Given: You have $\frac{dpm}{100 cm^2}$. You need to convert this to a flux ($\frac{\gamma}{cm^2 \cdot s}$). This requires knowing the gamma yield (Y, $\frac{\gamma}{dis}$) and assuming an emission geometry (e.g., $2\pi$ for a surface).
3. Build the Conversion Chain: $$\frac{mrem}{hr} = \left( \frac{dpm}{100 cm^2} \right) \times \left( \frac{1 dis}{dpm} \right) \times \left( \frac{Y \gamma}{dis} \right) \times \left( \frac{1 min}{60 s} \right) \times \left( \frac{60 min}{1 hr} \right) \times \left( \frac{100^2 cm^2}{m^2} \right) \times ...$$
4. Bridge Flux to Dose Rate: The final link is a flux-to-dose-rate conversion factor, which will be given in a form like $(\frac{mrem/hr}{\gamma/cm^2 \cdot s})$. By carefully arranging these factors, you can cancel all intermediate units and arrive at the desired final unit.

The Governing Differential Equation

Many complex operational problems (e.g., a radioactive gas leak into a ventilated room) can be modeled with a simple first-order differential equation. The rate of change of activity in a volume is the difference between the rate at which activity enters and the rate at which it is removed.

The key is to correctly define the **effective removal constant**, $\lambda_{eff}$. It is the sum of all removal constants:

Where $\lambda_{Ventilation}$ is the ventilation rate (in air changes per hour/minute) and $\lambda_{Other}$ could be a cleanup filter, etc.

Calculation & Unit Errors

• Unit Mismatches: The most common error. Forgetting to convert Ci to $\mu$Ci, hours to minutes, or cm to meters can change an answer by orders of magnitude. Always write out your units and make sure they cancel.
• Forgetting Buildup (B): Shielding calculations for broad beams always require a buildup factor. Forgetting it will result in an underestimate of the dose rate.
• $E_{avg}$ vs. $E_{max}$ for Betas: Dose calculations require the average beta energy ($E_{avg}$), which is roughly 1/3 of the maximum energy ($E_{max}$). Using $E_{max}$ will significantly overestimate the dose.
• Decay During Irradiation: Forgetting the $(1 - e^{-\lambda t_{irrad}})$ saturation factor when calculating activation will overestimate the final activity, especially when the irradiation time is short compared to the half-life.

Conceptual Errors

• Confusing Dose Quantities: Be precise with your terminology. Absorbed Dose (rad/Gy), Dose Equivalent (rem/Sv), and Exposure (R) are not interchangeable.
• Misinterpreting Statistical Tests: Remember that for MARSSIM, the null hypothesis ($H_0$) is that the area is dirty. The goal is to *reject* the null hypothesis to prove the area is clean.
• Ignoring Special Cases: Forgetting that some rules have exceptions (e.g., the need for low-Z material to shield high-energy betas first) is a common pitfall.

• ACGIH: American Conference of Governmental Industrial Hygienists - Sets occupational exposure limits for non-ionizing radiation (TLVs).
• ALI (Annual Limit on Intake): The activity of a radionuclide that, if inhaled or ingested, would result in a CEDE of 5 rem or a CDE of 50 rem to any organ.
• ALARA: As Low As Reasonably Achievable - The guiding principle of radiation protection.
• AMAD (Activity Median Aerodynamic Diameter): The median aerodynamic diameter of an aerosol, used to characterize particle size distribution for internal dosimetry.
• ANSI: American National Standards Institute - Develops consensus standards, including for laser safety (Z136.1).
• Buildup Factor (B): A correction factor used in shielding calculations to account for the contribution of scattered photons to the dose.
• BWR (Boiling Water Reactor): A type of nuclear reactor where water boils in the core, and the resulting steam directly drives a turbine.
• CDE / CEDE: Committed Dose Equivalent / Committed Effective Dose Equivalent - The dose received over 50 years from an intake of radioactive material.
• CPE (Charged Particle Equilibrium): A condition where the energy of charged particles leaving a volume is balanced by the energy of charged particles entering it. Under CPE, KERMA equals absorbed dose.
• Cross Section ($\sigma$): A measure of the probability of an interaction between a particle and a target nucleus, typically measured in barns ($10^{-24}$ cm²).
• DAC (Derived Air Concentration): The airborne concentration of a radionuclide that, if breathed for a working year, would result in an intake of one ALI.
• DCGL (Derived Concentration Guideline Level): A radionuclide concentration limit used in decommissioning to demonstrate that a site meets the release criterion (e.g., 25 mrem/yr).
• DDE (Deep Dose Equivalent): The external dose equivalent at a tissue depth of 1 cm (1000 mg/cm²).
• DQO (Data Quality Objective): A systematic planning process used in MARSSIM to ensure that the data collected will be sufficient to support the desired decision.
• HVL (Half-Value Layer): The thickness of a material required to reduce the intensity of a radiation beam to one-half its original value.
• ICRP: International Commission on Radiological Protection - An international body that provides recommendations and guidance on radiation protection.
• KERMA (Kinetic Energy Released in Media): The energy transferred from uncharged particles (photons, neutrons) to charged particles per unit mass of a medium.
• LET (Linear Energy Transfer): The rate at which a charged particle deposits energy as it travels through matter.
• MARSSIM: Multi-Agency Radiation Survey and Site Investigation Manual - A standardized methodology for decommissioning surveys.
• MPE (Maximum Permissible Exposure): The highest level of laser radiation to which a person can be exposed without hazardous effects.
• NCRP: National Council on Radiation Protection and Measurements - A U.S. organization that issues recommendations on radiation protection.
• NOHD (Nominal Ocular Hazard Distance): The distance from a laser at which the beam irradiance equals the MPE.
• PAG (Protective Action Guide): A projected dose at which a specific protective action (e.g., sheltering, evacuation) is recommended during an emergency.
• PWR (Pressurized Water Reactor): A type of nuclear reactor with separate primary (reactor) and secondary (turbine) coolant loops.
• Q-value: The total energy released in a nuclear reaction or decay.
• SAR (Specific Absorption Rate): The rate at which RF/microwave energy is absorbed per unit mass of body tissue.
• TEDE (Total Effective Dose Equivalent): The sum of the external deep dose equivalent (DDE) and the internal committed effective dose equivalent (CEDE).
• TLV (Threshold Limit Value): Exposure guidelines for occupational health hazards, including non-ionizing radiation, issued by the ACGIH.
• TVL (Tenth-Value Layer): The thickness of a material required to reduce the intensity of a radiation beam to one-tenth its original value.
• WRS (Wilcoxon Rank Sum) Test: A statistical test used in MARSSIM when the contaminant is also present in the background.